ESERCITAZIONI

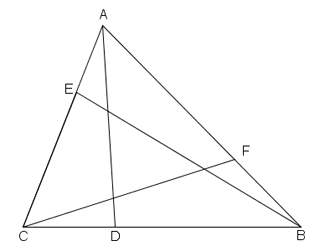
In un triangolo ABC, i punti D, E ed F sono presi sui lati BC, CA e AB, rispettivamente, in modo che



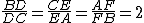
Dimostrare che il triangolo formato dai degmenti AD, BE e CF ha area 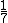dell'area del triangolo ABC.

Tratto da: Notes on Euclidean Geometry Kiran Kedlaya 1999
Problema 3 per la Sezione 1.1, pag. 2

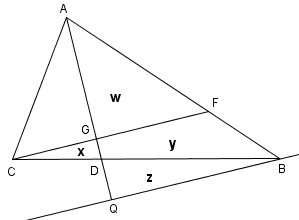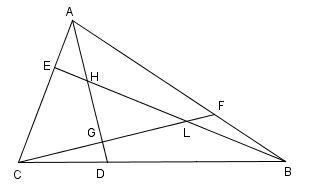
Tracciamo da B la parallela a CF ed indichiamo con Q il punto in cui tale retta interseca la semiretta AD.
Sia A l'area del triangolo ABC e siano x, y, z e w le aree dei poligoni, come indicato della figura.
Si hanno le seguenti relazioni:
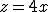(i triangoli BQD e CDG sono simili con rapporto 2)
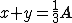(il triangolo CBF ha base 1/3 e stessa altezza del triangolo ABC)
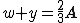(il triangolo ABD ha base 2/3 e stessa altezza del triangolo ABC)
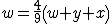(i triangoli AGF e AQB sono simili con rapporto 2/3).
Eliminando da queste uguaglianze y, z e w, si ottiene .
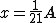La stessa area hanno, ovviamente, anche i triangoli LBF e EAH.
L'area del triangolo HGL si ottiene per sottrazione:

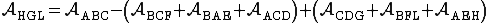
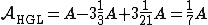
E' pervenuta una ulteriore dimostrazione, che utilizza equiscomposizione e similitudine si veda il file pdf

Per una generalizzazione a 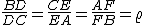si veda il file pdf

Una dimostrazione che utilizza direttamente l'equiscomposizione del triangolo in sette parti equivalenti, si veda il file pdf

» dimostrazione geometria » triangolo » area