ESERCITAZIONI

Sei in: root / Il problema della settimana


Lista dei problemi

8. Testo dell'esercizio

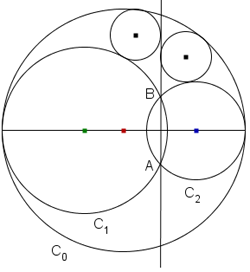
Nella figura i centri delle circonferenze C0, C1 e C2 sono allineati e C1 e C2 sono tangenti a C0.

A e B sono i punti di intersezione di C1 e C2.

Dimostrare che sono congruenti la circonferenza tangente a C0, C1 e ad AB e la circonferenza tangente a C0, C2 e ad AB.

Tratto da: International Mathematical Talent Search
Round 20 problema 5

8. Risoluzione

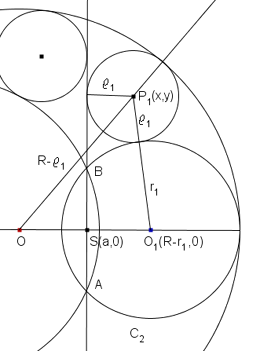
Soluzione analitica.

Assumiamo le coordinate rispetto l'origine il centro O delle circonferenza C0 e l'asse x la retta dei centri delle circonferenze.

Poniamo:
R il raggio della circonferenza C0
r1 il raggio della circonferenza C1
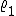latex: \large \varrho_{1} il raggio della circonferenza tangente a C0, C1 e ad AB
(x,y) le coordinate del suo centro P1
a l'ascissa del punto S in cui la retta AB interseca l'asse x.

In conseguenza alle condizioni di tangenza, x, y e 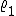latex: \large \varrho_{1} debbono soddisfare le equazioni

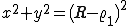
latex: \large x^2+y^2=(R-\varrho_{1})^{2}
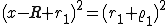
latex: \large (x-R+r_{1})^2=(r_{1}+\varrho_{1})^{2}

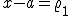
latex: \large x-a=\varrho_{1}

Il sistema, risolto, fornisce

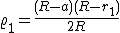
latex: \large \varrho_{1}=\frac{(R-a)(R-r_1)}{2R}

In modo analogo, si ottiene, per il raggio dell'altra circonferenza tangente, il valore

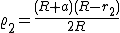
latex: \large \varrho_{2}=\frac{(R+a)(R-r_2)}{2R}

Uguagliando i due raggi, si ottiene la condizione:

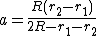
latex: \large a=\frac{R(r_2-r_1)}{2R-r_1-r_2}


Ma se calcolando a dall'intersezione delle due circonferenze, si ottiene proprio tale valore.

I calcoli nel dettaglio risoluzione del problema


E' pervenuta un'altra dimostrazione
risoluzione del problema

8. Tags

» dimostrazione geometria » circonferenza » circonferenze tangenti