ESERCITAZIONI

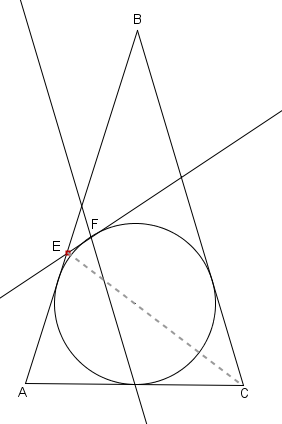In un triangolo ABC con AB = BC la retta parallela al lato BC e passante per il punto medio di AB interseca la circonferenza inscritta nel punto medio di AC e in un altro punto F.
Dimostrare che la tangente in F alla circonferenza inscritta e la bisettrice dell'angolo C si intersecano nello stesso punto del lato AB.

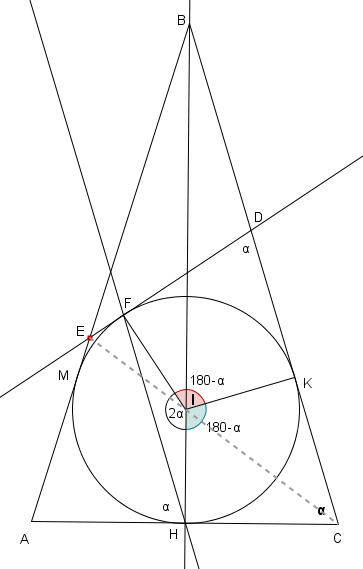Sia E in punto in cui la tangente in F alla circonferenza interna al triangolo interseca AB.
Dobbiamo dimostrare che CE è bisettrice dell'angolo interno C.
Sia I l'incentro del triangolo.
Con le notazioni in figura, per la tangenza si ha
EM ≅ EF
DF ≅ DK
CK ≅ CH
AH ≅ AM
Gli ultimi quattro segmenti sono inoltre congruenti, essendo AH ≅ CH.
Posto ,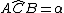
allora
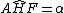per il parallelismo
(angolo al centro che insiste sull'arco HF, su cui insiste )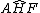
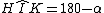(differenza di angoli nel quadrilatero HIKC)
Quindi
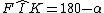(differenza di angoli nell'angolo giro in I)
Infine 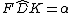(differenza di angoli nel quadrilatero FDKI).
Ne segue che il trapezio CHFD è isoscele e perciò CH ≅ FD.
Per transitività FD ≅ MA.
Quindi ED = EF + FD ed EA = EM + MA sono congruenti.
I triangoli ECA e ECD sono quindi congruenti e perciò EC è la bisettrice dell'angolo C.

• Una dimostrazione che utilizza le simmetrie della costruzione