ESERCITAZIONI
Sei in: root / Il problema della settimana
12. Testo dell'esercizio
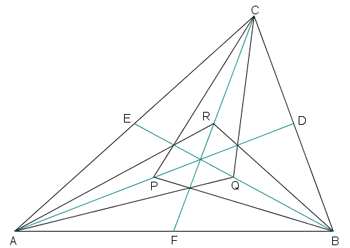
Nel triangolo ABC, siano D, E ed F i punti medi dei lati e siano P, Q ed R i punti medi delle mediane AD, BE e CF, rispettivamente, come mostrato in figura.
Dimostrare che il valore di
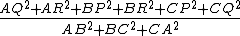
non dipende dal triangolo e trovare tale valore.
Tratto da:
International Mathematical Talent Search
Round 32 - problema 5
12. Risoluzione
Una risoluzione che utilizza il metodo delle coordinate viene fornita nel file pdf allegato
Risoluzione trigonometrica
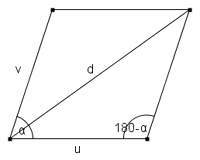
Premettiamo il calcolo della misura della diagonale di un paralleogramma conoscendo i due lati e l'angolo compreso. Per il teorema di Carnot, si ha
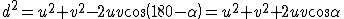
Indichiamo le misure dei lati e degli angoli del triangolo ABC con la consueta notazione goniometrica.
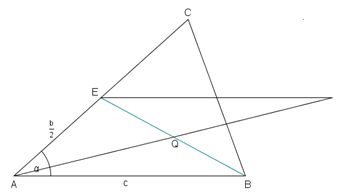 AQ è metà della diagonale del parallelogramma costruito su AB ed AE.
AQ è metà della diagonale del parallelogramma costruito su AB ed AE.
Si ha quindi
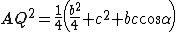
Analogamente, si ottiene per gli altri segmenti
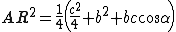
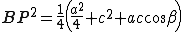
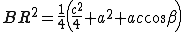
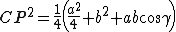
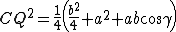
Le relazioni vengono addizionate membro a membro.
Per eliminare i termini che contengono gli angoli, si utilizzano le relazioni trigonometriche
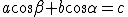
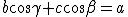
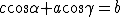
Si ottiene quindi
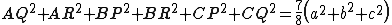
Il rapporto costante vale quindi