ESERCITAZIONI

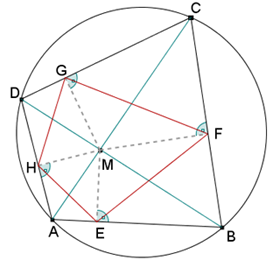
Sia ABCD un quadrilatero convesso inscritto in una circonferenza; sia M il punto di intersezione delle sue diagonali; siano E, F, G e H i piedi delle perpendicolari condotte da M ai lati di ABCD.
Determinare il centro della circonferenza inscritta nel quadrilatero EFGH.

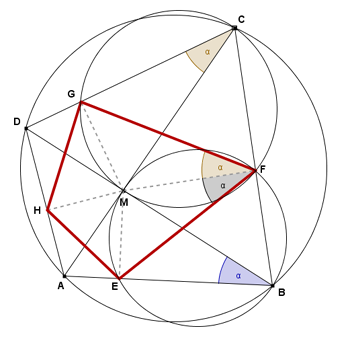
Il centro della circonferenza inscritta nel quadrilatero EFGH è il punto M stesso.

Considerata la circonferenza circoscritta al quadrilatero MFCG, si ha che 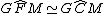perchè insistono sullo stesso arco GM

Considerata la circonferenza circoscritta al quadrilatero MFBE, si ha che 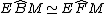perchè insistono sullo stesso arco EM

Considerata la circonferenza circoscritta al quadrilatero ABCD, si ha che 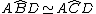perchè insistono sullo stesso arco AD

Per transitività  si ottiene che 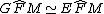e quindi EM è bisettrice dell'angolo .

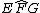Lo stesso si può dimostrare per gli altri angoli interni del quadrilatero EFGH.

Essendo intersezione delle bisettrici, M è il centro della circonferenza inscritta nel quadrilatero.