ESERCITAZIONI

Sei in: root / Il problema della settimana


Lista dei problemi

2. Testo dell'esercizio

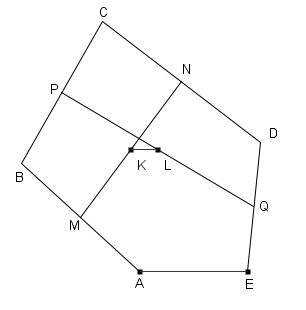Sia ABCDE un pentagono convesso e M, P, N e Q i punti medi dei lati AB, BC, CD, DE rispettivamente. Se K e L sono i punti medi di MN e PQ ed il segmento AE è di lunghezza a, trova la lunghezza del segmento KL.

Tratto da: IMO Bulgaria
Winter Mathematical Competition 1995 Problema 2

2. Soluzioni

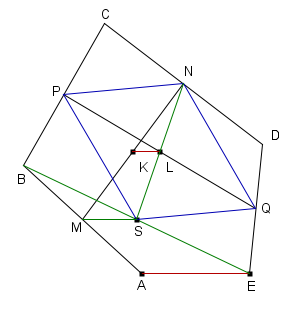
Tracciamo EB e sia S il suo punto medio.
Il quadrilatero PNQS è un parallelogramma (conseguenza del teorema di Talete) e NS ne è una diagonale, che quindi passa per il punto medio L dell'altra diagonale, PQ.
Nel triangolo MSN, KL ha estremi i punti medi di due lati. Perciò 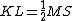latex: KL = \frac{1}{2}MS.
Nel triangolo AEB, MS ha estremi i punti medi di due lati. Perciò 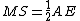latex: MS = \frac{1}{2}AE.
Di conseguenza 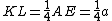latex: KL = \frac{1}{4}AE = \frac{1}{4}a.

Altre soluzioni:
soluzione con i vettori
soluzione con le coordinate

2. Tags

» poligoni » punto medio