ESERCITAZIONI
Sei in: root / Il problema della settimana
Lista dei problemi
18. Testo dell'esercizio
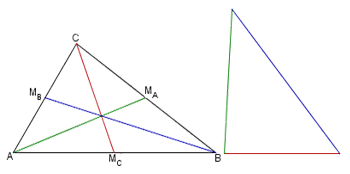 Sia ABC un triangolo e MA, MB e MC i punti medi dei lati BC, CA e AB, rispettivamente.
Sia ABC un triangolo e MA, MB e MC i punti medi dei lati BC, CA e AB, rispettivamente.Dimostrare che il triangolo con i lati lunghi AMA, BMB e CMC ha area 3/4 dell'area del triangolo ABC.
Tratto da:
Notes on Euclidean Geometry Kiran Kedlaya 1999
Problemi della sezione 1.1, n.2 - pag.1
Problemi della sezione 1.1, n.2 - pag.1
18. Risoluzione
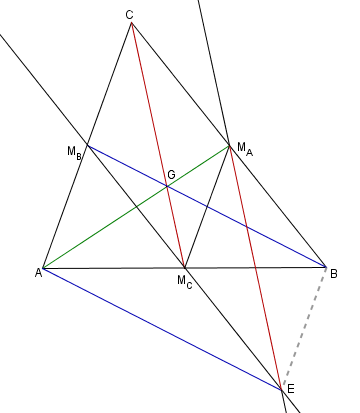 La parallela a CMC per MA incontra MBMC in E.
La parallela a CMC per MA incontra MBMC in E.CMAEMC è un parallelogramma (anche MBMC è parallela a BC).
Poichè MBMC è congruente a MAC e MCE è congruente a MAC allora MCE è congruente a MAC.
AMBBE è quindi un parallelogramma perchè le diagonali si intersecano a metà.
Di conseguenza AE è congruente a MBB.
Il triangolo AMAE ha quindi i lati congruenti alle mediane del triangolo ABC ed è unione dei triangoli AMCMA, MCMAE e AMCE, ciascuno dei quali ha area 1/4 dell'area del triangolo ABC.
Infatti:
AMCMA ha base e altezza la metà di quelle di ABC.
MCMAE è congruente a MCMAC, che ha base e altezza la metà di quelle di ABC.
AMCE è congruente a MBMCB, che ha base e altezza la metà di quelle di ABC.
La tesi è dimostrata.
Un'altra dimostrazione nel file pdf