ESERCITAZIONI
Sei in: root / Il problema della settimana
Lista dei problemi
16. Testo dell'esercizio
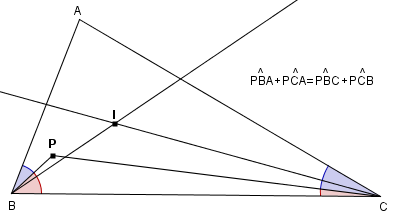 Sia ABC un triangolo e sia I il centro della sua circonferenza inscritta.
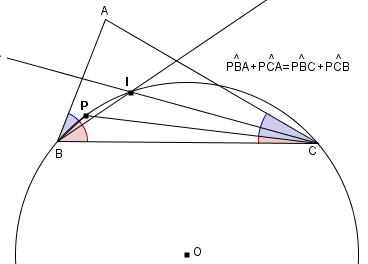
Sia ABC un triangolo e sia I il centro della sua circonferenza inscritta.Sia P un punto interno al triangolo tale che
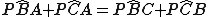
Tratto da:
International Mathematical Olympiad
12 luglio 2006 - Problema 1
16. Soluzioni
 L'ipotesi
L'ipotesi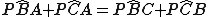
ed il fatto che
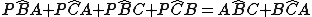
implicano che
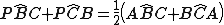 .
.Di conseguenza
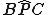 ha ampiezza costante al variare di P e P appartiene quindi all'arco di circonferenza luogo dei punti del piano che formano col segmento BC lo stesso angolo.
ha ampiezza costante al variare di P e P appartiene quindi all'arco di circonferenza luogo dei punti del piano che formano col segmento BC lo stesso angolo.Dal momento che il centro I della circonferenza inscritta è l'intersezione delle bisettrici, allora
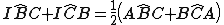 ,
,
allora I è un possibile punto P e quindi l'arco di circonferenza in questione è la circonferenza per B, C ed I.
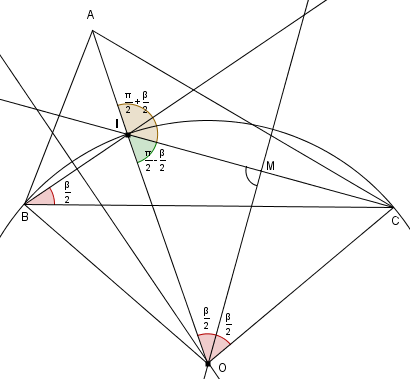 Dimostriamo che il centro O di tale circonferenza è allineato con A e I.
Dimostriamo che il centro O di tale circonferenza è allineato con A e I.Poniamo
 .
.Si ha
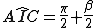 (proprietà dell'incentro)
(proprietà dell'incentro)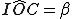 (angolo al centro che insiste sullo stesso arco IC dell'angolo
(angolo al centro che insiste sullo stesso arco IC dell'angolo 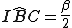 )
)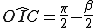 (triangolo rettangolo generato dall'asse di IC)
(triangolo rettangolo generato dall'asse di IC)Quindi

Di conseguenza I è l'unico punto della circonferenza a minor distanza dal vertice A e quindi è vera sia la tesi
Sono pervenute le soluzioni