ESERCITAZIONI
Sei in: root / Il problema della settimana
11. Testo dell'esercizio
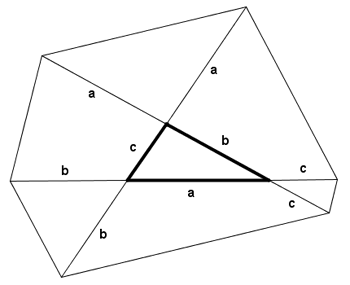
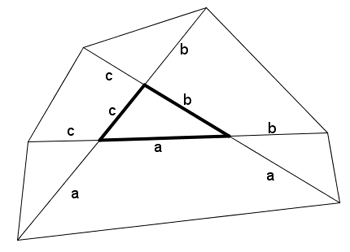
E' dato un triangolo ABC.
Prolungare i suoi lati e costruire due esagoni come mostrato nelle figure.
Comparare le aree degli esagoni.
Tratto da:
International Mathematical Talent Search
Round 14 problema 5
11. Risoluzione
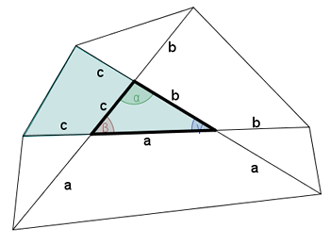
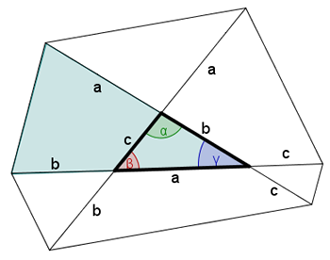
Risoluzione trigonometrica
Nel primo caso, consideriamo i triangoli isosceli che si formano con i prolungamenti (in figura ne viene mostrato uno).
L'area dell'esagono è data dalla somma di queste tre aree alla quale debbono essere addizionate le aree dei tre triangoli isosceli che si formano con i prolungamenti e deve essere sottratta due volte l'area del triangolo (detta A nella formula).

In ogni triangolo si hanno le relazioni goniometriche
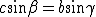
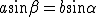
Utilizzando queste relazioni, possiamo eliminare due angoli.
Eliminiamo, ad esempio,  e
e 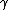 .
.
Otteniamo
![latex: \large A_1 = \frac{\sin\beta}{2b}\left[c(a+b)^2+ a(b+c)^2 + b(a+c)^2 + b^3 + c^3 + a^3 - 2abc\right]](https://www.diflo.it/esercitazioni/cache/c0012/e79cea124c51ce9a4bc9263930c5d940.gif )
nel quale l'ultimo termine tra parentesi si ottiene dall'area del triangolo.
Facendo i calcoli, si ottiene
![latex: \large A_1 = \frac{\sin\beta}{2b}\left[a^3 + b^3 + c^3 + a^2b + a^2c + b^2a + b^2c + c^2a + c^2b + 4abc\right]](https://www.diflo.it/esercitazioni/cache/c0012/444ab6c9a88143191c34d65c8619dccf.gif )
Nel secondo caso, consideriamo i triangoli che si formano con i prolungamenti (in figura ne viene mostrato uno).
L'area dell'esagono è data dalla somma di queste tre aree a cui debbono essere addizionate le aree dei tre triangoli congruenti a quello iniziale che si formano con i prolungamenti e deve essere sottratta due volte l'area del triangolo (detta A nella formula). In pratica, l'area A viene sommata una volta.
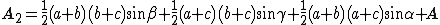
Ripetendo i passaggi del caso precedente, si arriva la stessa formula per A1
E' pervenuta un'altra dimostrazione
risoluzione del problema