ESERCITAZIONI

Sei in: root / Il problema della settimana


Lista dei problemi

2. Testo dell'esercizio


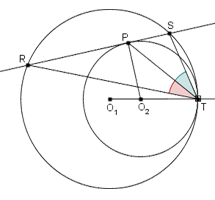
Due circonferenze sono tangenti internamente in T.
Una retta è tangente in P alla circonferenza interna ed interseca quella esterna nei punti R e S.
Dimostrare che TP è bisettrice dell'angolo RTS.



Tratto da: BRITISH MATHEMATICAL OLYMPIAD
Round 1 : Wednesday 13th January 1993 problema 4

2. Risoluzione


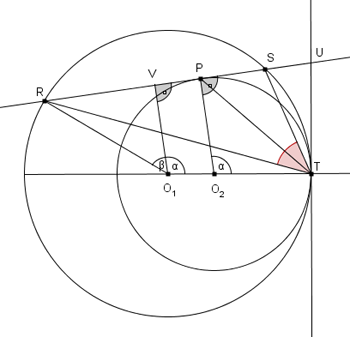
Tracciamo l'asse della corda RS e la tangente in T alle circonferenze.

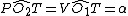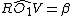
Poniamo latex: P\widehat{O_2}T=V\widehat{O_1}T=\alpha e latex: R\widehat{O_1}V=\beta

Si ha:
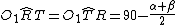
latex: O_1\widehat{R}T=O_1\widehat{T}R=90-\frac{\alpha+\beta}{2}
(differenza angoli nel triangolo isoscele RO1T)

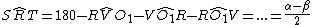
latex: S\widehat{R}T=180-R\widehat{V}O_1-V\widehat{O_1}R-R\widehat{O_1}V=...=\frac{\alpha-\beta}{2}
(differenza angoli nel triangolo rettangolo RO1V)

latex: S\widehat{T}U=S\widehat{R}T=\frac{\alpha-\beta}{2}
(angoli alla circonferenza che insistono sullo stesso arco TS)

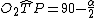latex: O_2\widehat{T}P=90-\frac{\alpha}{2} (differenza angoli nel triangolo isoscele PO2T)

Quindi, per differenza:
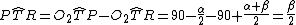
latex: P\widehat{T}R=O_2\widehat{T}P-O_2\widehat{T}R=90-\frac{\alpha}{2}-90+\frac{\alpha+\beta}{2}=\frac{\beta}{2}

E, infine, sempre per differenza:
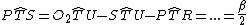
latex: P\widehat{T}S=O_2\widehat{T}U-S\widehat{T}U-P\widehat{T}R=...=\frac{\beta}{2}

E quindi si ottiene la tesi.

2. Tags

» dimostrazione geometria » circonferenza » circonferenze tangenti » angoli in circonferenze