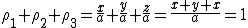ESERCITAZIONI

Sei in: root / Il problema della settimana


Lista dei problemi

1. Testo dell'esercizio

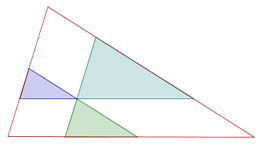
Da un punto interno ad un triangolo di area T si tracciano le parallele ai lati, che suddividono il triangolo in tre triangoli e tre parallelogrammi.
Dette T1, T2 e T3 le aree dei triangoli, dimostrare che

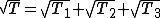
latex: \large \sqrt{T}=\sqrt{T_1}+\sqrt{T_2}+\sqrt{T_3}



Tratto da: Notes on Euclidean Geometry Kiran Kedlaya 1999
pag. 75 - problema indicato con: Sweden, 1996

1. Risoluzione


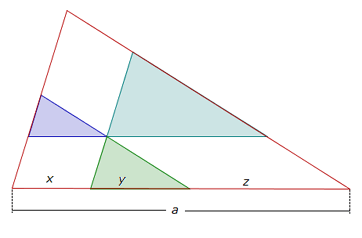
I tre triangoli sono simili al triangolo ABC.

Detti 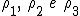latex: \large \rho_{1},\:\rho_{2} \:e\: \rho_{3} i tre rapporti di similitudine, sappiamo che tra le aree valgono le relazioni

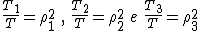
latex: \large \frac{T_{1}}{T} = \rho_{1}^{2} \:,\: \frac{T_{2}}{T} = \rho_{2}^{2} \: e \: \frac{T_{3}}{T} = \rho_{3}^{2}

da cui

latex: \large \sqrt[]{\frac{T_{1}}{T}} = \rho_{1} \:,\: \sqrt[]{\frac{T_{2}}{T}} = \rho_{2} \: e \: \sqrt[]{\frac{T_{3}}{T}} = \rho_{3}

latex: \large \sqrt[]{T_{1}} = \rho_{1} \cdot \sqrt[]{T} \:,\: \sqrt[]{T_{2}} = \rho_{2} \cdot \sqrt[]{T} \: e \: \sqrt[]{T_{3}} = \rho_{3} \cdot \sqrt[]{T}

e, sommando le uguaglianze

latex: \large \sqrt[]{T_{1}} + \sqrt[]{T_{2}} + \sqrt[]{T_{3}} = \rho_{1} \cdot \sqrt[]{T} + \rho_{2} \cdot \sqrt[]{T} + \rho_{3} \cdot \sqrt[]{T}

e, infine,

latex: \large \sqrt[]{T_{1}} + \sqrt[]{T_{2}} + \sqrt[]{T_{3}} = \left( \rho_{1} + \rho_{2} + \rho_{3} \right) \cdot \sqrt[]{T}

Resta da dimostrare che

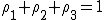
latex: \large \rho_{1} + \rho_{2} + \rho_{3} = 1

Usando le misure in figura, si ha

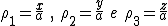
latex: \large \rho_{1} = \frac{x}{a} \:,\: \rho_{2} = \frac{y}{a} \:e\: \rho_{3} = \frac{z}{a}

Quindi: latex: \large \rho_{1} + \rho_{2} + \rho_{3} = \frac{x}{a} + \frac{y}{a} + \frac{z}{a} = \frac{x+y+x}{a} = 1

1. Tags

» dimostrazione geometria » triangolo » triangoli simili » area