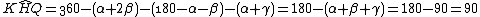ESERCITAZIONI

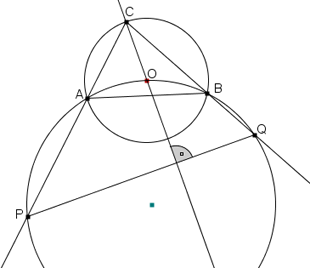Sia ABC un triangolo acutangolo, sia C₁ la circonferenza circoscritta e sia O il suo circocentro. Chiamiamo C₂ la circonferenza per A,O e B. Le rette CA e CB incontrano C₂ anche in P e Q, rispettivamente.
Dimostrare che le rette CO e PQ sono perpendicolari.

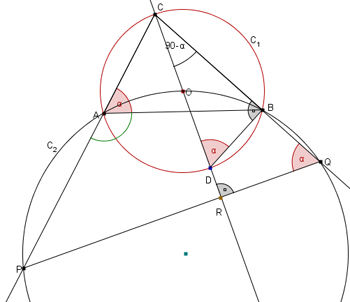
Sia D il punto in cui la semiretta CO interseca la circonferenza C₁.

Poichè insistono entrambi sull'arco BC, si ha che



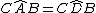
Il quadrilatero ABQP è inscritto nella circonferenza C₂ e, di conseguenza l'angolo 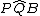è supplementare dell'angolo , che è angolo adiacente a .
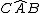Quindi, per transitività,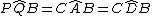

I triangolo CDB e CQR hanno quindi due angoli congruenti e di conseguenza anche il terzo.
Essendo il triangolo CDB rettangolo in B (CD è un diametro) allora ne segue che QHC è rettangolo in R.

Altra dimostrazione

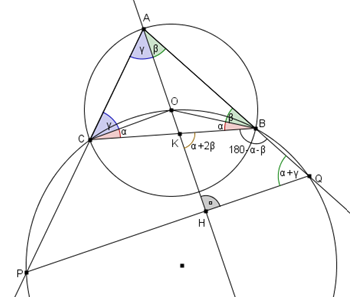
Con le notazioni in figura si ha che

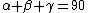perchè i triangoli OAC, OAB e OBC sono isosceli.

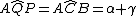per la similitudine dei triangoli ABC e APQ (angolo in comune e due coppie di lati proporzionali per il teorema delle secanti)

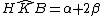, per il teorema dell'angolo esterno.

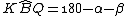(angolo adiacente)

Nel quadrilatero KBQH possiamo calcolare quindi il quarto angolo: