ESERCITAZIONI

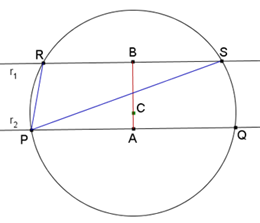
Nella figura, r₁ e r₂ sono due rette parallele e A e B due punti presi su ciascuna di esse in modo che il segmento AB sia perpendicolare ad esse.
Si costruisce la circonferenza di centro un qualunque punto C di AB e diametro un segmento (fissato) maggiore di AB.
Dette P, Q, R ed S le intersezioni della circonferenza con le rette r₁ e r₂, dimostrare che il prodotto PR · PS è indipendente dalla scelta di C sul segmento AB.

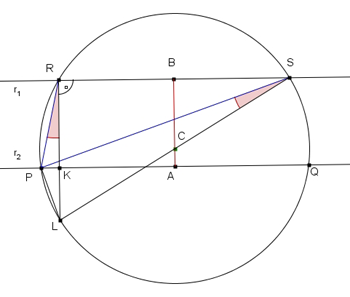
Tracciare il diametro SL e congiungere L con R.
Detta K l'intersezione tra LR e PQ, i triangoli PKR e LPS sono simili.

Infatti: in quanto insistono entrambi sull'arco PL.

Inoltre 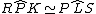in quanto insistono sugli archi congruenti QR e SP (addizione di archi congruenti).

La relazione cercata segue dalla proporzione PR : SL = RK : PS
dalla quale PR · PS = SL · RK
ed il secondo prodotto è costante essendo SL il diametro (costante per ipotesi) della circonferenza e RK = AB, anch'esso costane.