ESERCITAZIONI

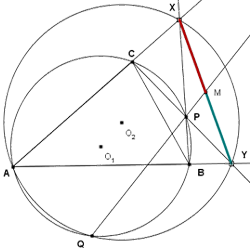
Sia P un punto sulla circonferenza circoscritta al triangolo ABC, diverso da A, B e C.
Supponiamo che BP intersechi AC in X e che CP intersechi AB in Y.
Sia Q il punto di intersezione delle circonferenze circoscritte ai triangoli ABC e AXY, con Q diverso da A.
Dimostra che PQ incontra il segmento XY nel punto medio di XY.
(I vari punti di intersezione possono stare sui prolungamenti dei segmenti)

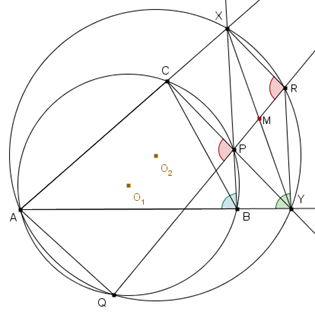
Prolungare QP fino ad incontrare la circonferenza circoscritta ad AXY in R.

Si dimostra che PYRX è un parallelogramma, e, di conseguenza, la tesi segue dal fatto che M è il punto di intersezione delle sue diagonali.

Se consideriamo i quadrilateri AQPC e AQRX inscritti nelle circonferenze, essi hanno gli angoli opposti supplementari; quindi gli angoli nei vertici P ed R sono congruenti in quanto entrambi supplementari all'angolo nel vertice A.
Di conseguenza, sono parallele le rette PY e XR.

Nella circonferenza circoscritta a ABC si che 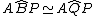perchè insistono entrambi sul medesimo arco AP.
Analogamente, nella circonferenza circoscritta a AXY si che 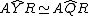perchè insistono sul medesimo arco AR.
Ovviamente gli angoli in Q sono gli stessi e quindi .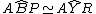
Quindi sono parallele le rette PX e YR.