ESERCITAZIONI

Sei in: root / Il problema della settimana


Lista dei problemi

22. Testo dell'esercizio

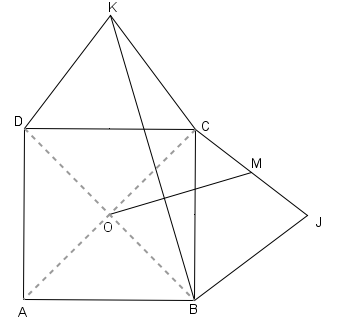
Sia ABCD un quadrato di centro O. Si costruiscano due triangoli isosceli BCJ e CDK, esterni al quadrato, di base BC e CD rispettivamente e congruenti fra loro. Sia poi M il punto medio di CJ.
Si provi che le rette OM e BK sono perpendicolari.



Tratto da: Finale delle Olimpiadi italiane di Matematica, Cesenatico 2009 1999
9 maggio 2009 - problema 2

22. Risoluzione

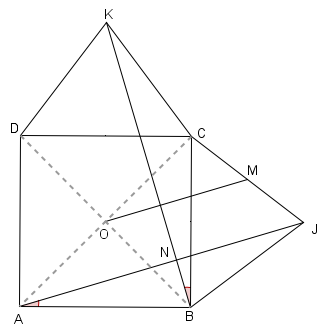
Osserviamo che AO=OC e JM=MC, per cui OM||AJ.
E' quindi sufficiente dimostrare la perpendicolarità tra AJ e BK.
Il triangolo KCB è congruente al triangolo ABJ (due lati e l'angolo compreso).
Quindi 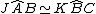latex: J\hat{A}B \simeq K\hat{B}C
Essendo 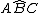latex: A\hat{B}C retto ne segue che 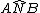latex: A\hat{N}B è retto.

22. Tags

» teorema di Talete » quadrato » triangolo isoscele