ESERCITAZIONI

Sei in: root / Il problema della settimana


Lista dei problemi

17. Testo dell'esercizio

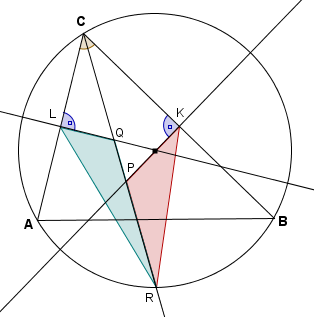In un triangolo ABC la bisettrice dell'angolo latex: B\hat{C}A interseca la circonferenza circoscritta in R (R ≠ C), l'asse di BC in P, e l'asse di AC in Q. Il punto medio di BC è K e il punto medio di AC è L. Dimostrare che i triangoli RPK e RQL hanno la stessa area.

Tratto da: International Mathematical Olympiad
2007 - secondo giorno - problema 4

17. Risoluzione

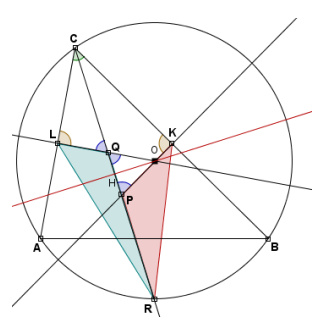Dimostriamo innanzitutto che

CQ=PR e CP=RQ

Infatti, l'intersezione dei due assi è il centro O della circonferenza e di conseguenza l'asse della corda CR dimezza la corda stessa nell'intersezione H. Inoltre, per le ipotesi sugli angoli della costruzione, il triangolo OQP è isoscele e quindi H dimezza anche QP.
Quindi CQ=CH-QH=HR-HP=PR
e CP=CQ+QP=PR+QP=QR.
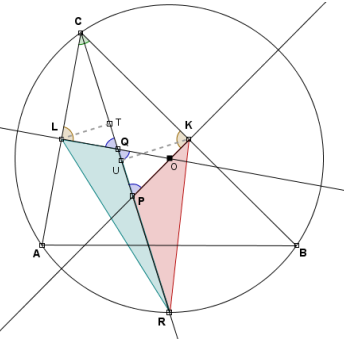Siano LT e KU le altezza dei triangolo rispetto le basi QR e, rispettivamente, PR.
I triangoli CQL e CKP sono simili e perciò
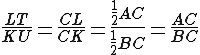
latex: \Large \frac{LT}{KU} = \frac{CL}{CK} = \frac{\frac{1}{2}AC}{\frac{1}{2}BC} = \frac{AC}{BC}
Inoltre, per quanto dimostrato in precedenza:
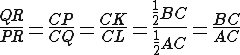
latex: \Large \frac{QR}{PR} = \frac{CP}{CQ} = \frac{CK}{CL} = \frac{\frac{1}{2}BC}{\frac{1}{2}AC} = \frac{BC}{AC}
I triangoli RPK e RQL hanno quindi la stessa area, avendo rapporto tra le basi inverso del rapporto tra le altezze.

17. Tags

» dimostrazione geometria » circonferenza circoscritta