ESERCITAZIONI

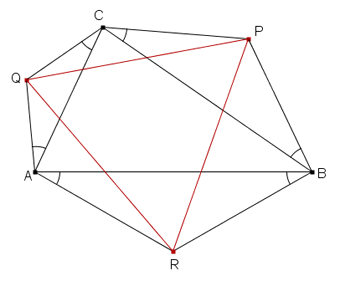
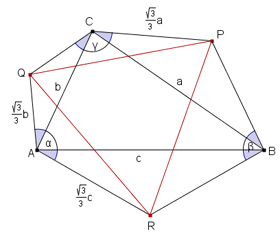
Sia ABC un arbitrario triangolo e costruire i punti P, Q e R tali che ciascuno degli angoli segnati in figura risultino di 30 °.
Dimostrare che il triangolo PQR è equilatero.

Tratto da: International Mathematical Talent Search
Round 4 - problema 4

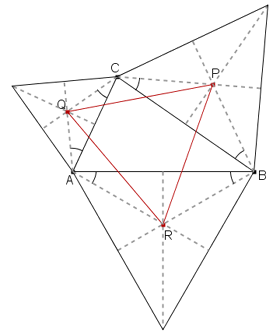
Osserviamo innanzitutto che l'esercizio è, in pratica, il cosiddetto teorema di Napoleone, la cui ipotesi richiede la costruzione dei triangoli equilateri su ciascuno dei lati del triangolo ABC ed il triangolo PQR che deve essere dimostrato equilatero è quello i cui vertici sono i centri di tali triangoli equilateri.

Dimostrazione trigonometrica

Indichiamo i lati e gli angoli del triangolo con la notazione standard della trigonometria (vedi figura).

Innanzitutto, i lati uguali dei triangoli isosceli ACQ, ABR e BCP si ottengono moltiplicando per 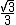le misure del triangolo ABC (teorema dei seni).

Il teorema di Carnot applicato ai triangoli ARQ, BPR e CQP dà le seguenti relazioni







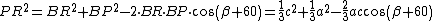
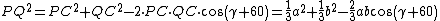
Le tre formule nel triangolo danno lo stesso valore.
Trasformiamo, ad esempio, la prima nella seconda (si è omesso il coefficiente ).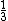




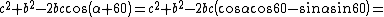
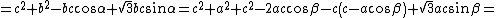
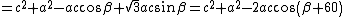
Si è usato

il teorema di Carnot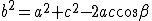

e le identità nel triangolo