ESERCITAZIONI
Sei in: root / Il problema della settimana
13. Testo dell'esercizio
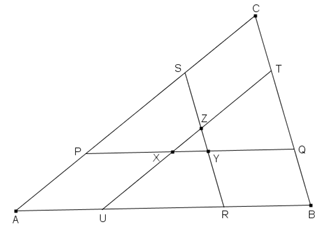
Nel triangolo ABC, i segmenti PQ, RS e TU sono paralleli ai lati AB, BC e CA, rispettivamente, e si intersecano nei punti X, Y e Z, come mostrato in figura.
Determinare l'area di ABC se ciascuno dei segmenti PQ, RS e TU divide l'area di ABC in due parti equivalenti e se l'area del triangolo XYZ č una unitā.
La risposta deve essere data nella forma 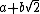 dove a e b sono numeri interi positivi.
dove a e b sono numeri interi positivi.
Tratto da:
International Mathematical Talent Search
Round 38 - problema 5
13. Risoluzione
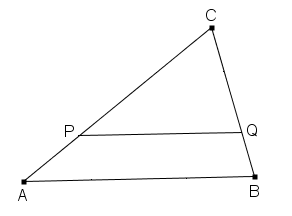
Se un segmento PQ è parallelo al lato AB di un triangolo e lo divide in due parti equivalenti, allora, poichè la parte triangolare PQC è simile al triangolo ABC, il rapporto di similitudine deve soddisfare la seguente relazione con le aree dei triangoli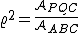
Poichè il rapporto tra le aree deve essere uguale a 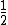 allora deve essere
allora deve essere ![latex: \large \varrho = \frac{\sqrt[]{2}}{2}](https://www.diflo.it/esercitazioni/cache/c0014/181bbead173fd8fe62deaf214757c220.gif )
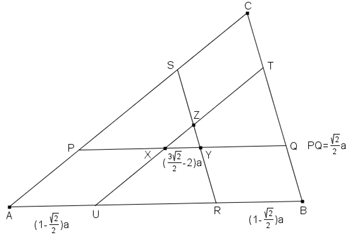 Poichè lo stesso succede con gli altri lati TU ed SR, allora i triangoli PQC, UTB e ARS, essendo simili ad ABC con lo stesso rapporto, sono congruenti, e perciò AR=UB=PQ.
Poichè lo stesso succede con gli altri lati TU ed SR, allora i triangoli PQC, UTB e ARS, essendo simili ad ABC con lo stesso rapporto, sono congruenti, e perciò AR=UB=PQ.
Detto AB = a, deve essere 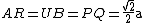
Di conseguenza, ![latex: PX = AU = YQ = RB = \left( 1 - \frac{\sqrt[]{2}}{2} \right) \text{a}](https://www.diflo.it/esercitazioni/cache/c0014/03e1874edabd2b41394833b2c5dd3c45.gif ) .
.
Ne segue che ![latex: XY = PQ - PX - YQ = \left(\frac{3\sqrt[]{2}}{2} - 2 \right) \text{a}](https://www.diflo.it/esercitazioni/cache/c0014/211972a7a8987c7e623ad323c543e73f.gif ) .
.
E quindi ![latex: \frac{3\sqrt[]{2}}{2} - 2](https://www.diflo.it/esercitazioni/cache/c0014/e9bf686ecffc6475b2acc2293ce2d70d.gif ) è il rapporto di similitudine tra i triangoli XYZ e ABC.
è il rapporto di similitudine tra i triangoli XYZ e ABC.
Ne segue che tra le aree si ha ![latex: \large \left( \frac{3\sqrt[]{2}}{2} - 2 \right)^2 = \frac{\mathcal{A}_{XYZ}}{\mathcal{A}_{ABC}}](https://www.diflo.it/esercitazioni/cache/c0014/7785a48d014615eb14831c6e2254d57b.gif )
Poichè l'area del triangolo XYZ è una unità, allora si ha
![latex: \large \mathcal{A}_{ABC} = \frac{1}{\left( \frac{3\sqrt[]{2}}{2} - 2 \right)^2}=\frac{1}{\left( \frac{3\sqrt[]{2}}{2} - 2 \right)^2} \cdot \frac{\left( \frac{3\sqrt[]{2}}{2} + 2 \right)^2}{\left( \frac{3\sqrt[]{2}}{2} + 2 \right)^2}= 34+24\sqrt[]{2} \approx 68](https://www.diflo.it/esercitazioni/cache/c0014/9cfef827b1bfb1b9f9aca4521b4878bc.gif )