ESERCITAZIONI

Sei in: root / Il problema della settimana

Lista dei problemi

« 1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 »

10. Testo dell'esercizio

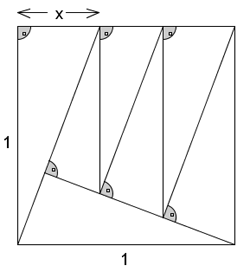
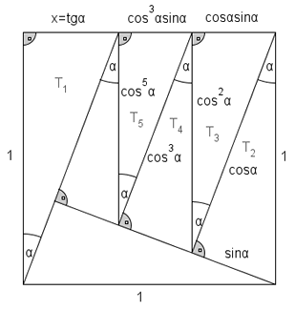
C'è un numero reale x, 0 < x < 1, tale che la configurazione mostrata in figura costituisce una suddivisione del quadrato unitario in sette triangoli rettangoli simili.
Questo x deve soddisfare ad un'equazione di quinto grado. Trovare l'equazione.

Tratto da: International Mathematical Talent Search
Round 8 problema 2

10. Risoluzione

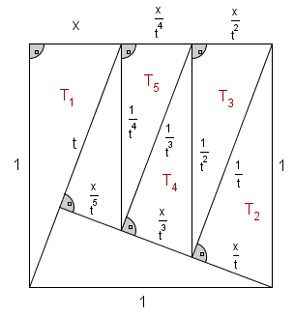
Risoluzione algebrica

Sia $latex: \large t = \sqrt[]{1+x^2}$ l'ipotenusa del triangolo T₁.

Il rapporto di similitudine tra i triangoli T₁ e T₂ è 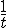$latex: \Large \frac{1}{t}$ e così tra un triangolo e quello successivo.

Quindi i cateti dei triangoli T₁, T₃ e T₅ sommati danno l'equazione

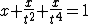
$latex: \large x + \frac{x}{t^2} + \frac{x}{t^4} = 1$

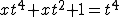
$latex: \large xt^4 + xt^2 + 1 = t^4$

e, sostituendo a t l'espressione in x e riordinando, si ottiene l'equazione:

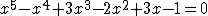
$latex: \large x^5 - x^4 + 3x^3 - 2x^2 + 3x -1 = 0$

La soluzione vale circa x = 0,378915...

Risoluzione trigonometrica

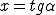Sia $latex: \large x = tg\alpha$ .
Le varie misure sono in figura e l'equazione trigonometrica ottenuta è

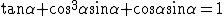
$latex: \large \tan\alpha+\cos^{3}\alpha\sin\alpha+\cos\alpha\sin\alpha=1$

che diventa:

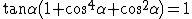
$latex: \large \tan\alpha(1+\cos^{4}\alpha+\cos^{2}\alpha)=1$

Usando la relazione tra coseno e tangente: 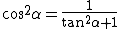$latex: \large \cos^{2}\alpha=\frac{1}{\tan^{2}\alpha+1}$

si ottiene l'equazione di quinto grado in 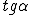$latex: \large tg\alpha$ cioè in x.

10. Tags

» dimostrazione geometria » triangolo » triangoli simili